{{{sourceTextContent.title}}}

Qu'est-ce que l'erreur d'Abbé et comment affecte-t-elle les systèmes de mouvement linéaire ?

{{{sourceTextContent.subTitle}}}

Les erreurs d'abbé commencent comme des erreurs angulaires.

{{{sourceTextContent.description}}}

Lorsqu'on évalue la précision d'un système de mouvement linéaire, on se concentre souvent sur la précision de positionnement et la répétabilité du mécanisme d'entraînement. Mais de nombreux facteurs contribuent à la précision (ou à l'imprécision) d'un système linéaire, notamment les erreurs linéaires, les erreurs angulaires et les erreurs d'Abbé. De ces trois types, les erreurs d'Abbé sont probablement les plus difficiles à mesurer, à quantifier et à prévenir, mais elles peuvent être la cause la plus importante de résultats indésirables dans les applications d'usinage, de mesure et de positionnement de haute précision.

Les erreurs d'Abbé commencent comme des erreurs angulaires

Les erreurs d'abbé sont causées par la combinaison d'erreurs angulaires dans le système de mouvement et du décalage entre le point d'intérêt (outillage, charge, etc.) et l'origine de l'erreur (vis, glissière, etc.).

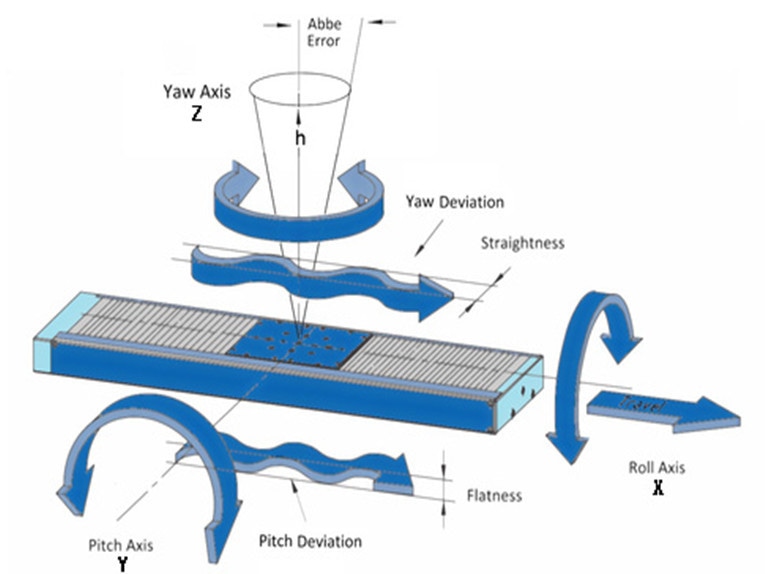
Les erreurs angulaires - communément appelées roulis, tangage et lacet - sont des mouvements indésirables dus à la rotation d'un système linéaire autour de ses trois axes.

Si un système se déplace horizontalement le long de l'axe X, comme illustré ci-dessous, le tangage est défini comme la rotation autour de l'axe Y, le lacet est la rotation autour de l'axe Z et le roulis est la rotation autour de l'axe X.

Les erreurs de roulis, de tangage et de lacet résultent généralement d'imprécisions dans le système de guidage, mais les surfaces et méthodes de montage peuvent également être des sources d'erreurs angulaires. Par exemple, les surfaces de montage qui ne sont pas usinées avec précision, les composants qui ne sont pas suffisamment fixés, ou même les taux variables de dilatation thermique entre le système et sa surface de montage peuvent tous contribuer à des erreurs angulaires supérieures à celles inhérentes aux guides linéaires eux-mêmes.

Les erreurs Abbé sont particulièrement problématiques parce qu'elles amplifient ce qui, dans la plupart des cas, sont de très petites erreurs angulaires, augmentant en magnitude au fur et à mesure que la distance du composant causant l'erreur (appelée décalage Abbé) augmente.

Dans l'illustration de droite, le décalage Abbé est h. La quantité d'erreur Abbé, δ, peut être déterminée à l'aide de l'équation suivante :

δ = h * tan θ

Pour les charges en porte-à-faux, plus la charge est éloignée de la cause de l'erreur angulaire (généralement le rail de guidage ou un point sur la surface de montage), plus l'erreur d'Abbé sera élevée. Et pour les configurations multi-axes, les erreurs d'Abbé sont encore plus complexes car elles sont aggravées par la présence d'erreurs angulaires sur chaque axe.

Les meilleures méthodes pour minimiser les erreurs d'Abbé consistent à utiliser des guides de haute précision et à s'assurer que les surfaces de montage sont suffisamment usinées pour ne pas introduire d'inexactitudes supplémentaires dans le système. Réduire le décalage d'Abbé en déplaçant la charge aussi près que possible du centre du système minimisera également les erreurs d'Abbé.

Les erreurs d'Abbé sont mesurées avec plus de précision à l'aide d'un interféromètre laser ou d'un autre dispositif optique totalement indépendant du système. Mais les interféromètres laser ne sont pas pratiques pour la plupart des configurations, de sorte que les codeurs linéaires sont utilisés dans de nombreuses applications où l'erreur d'Abbé est un problème. Dans ce cas, les mesures les plus précises de l'erreur Abbé sont obtenues lorsque la tête de lecture du codeur est montée sur le point d'intérêt - c'est-à-dire l'outillage ou la charge.

Les tables XY sont moins sujettes aux erreurs d'Abbé que d'autres types de systèmes multi-axes (tels que les robots cartésiens), principalement parce qu'elles minimisent la quantité de déplacement en porte-à-faux et fonctionnent généralement avec la charge située au centre du chariot d'axe Y.